Min of Three Part 2 Mar 18, 2017

This is the continuation of the previous post about optimizing 2D grid based dynamic programming algorithm for CPU level parallelism.

In The Previous Episode

This is the code we are trying to make faster:

fn dtw(xs: &[f64], ys: &[f64]) -> f64 {
    // assume equal lengths for simplicity
    assert_eq!(xs.len(), ys.len());
    let n = xs.len();
    let mut prev = vec![0f64; n + 1];
    let mut curr = vec![std::f64::MAX; n + 1];
    curr[0] = 0.0;

    for ix in 1..(n + 1) {
        ::std::mem::swap(&mut curr, &mut prev);
        curr[0] = std::f64::MAX;
        for iy in 1..(n + 1) {
            let d11 = prev[iy - 1];
            let d01 = curr[iy - 1];
            let d10 = prev[iy];

            // Find the minimum of d11, d01, d10
            // by enumerating all the cases.
            let d = if d11 < d01 {
                if d11 < d10 { d11 } else { d10 }
            } else {
                if d01 < d10 { d01 } else { d10 }
            };

            let cost = {
                let t = xs[ix - 1] - ys[iy - 1];
                t * t
            };

            curr[iy] = d + cost;
        }
    }
    curr[n]
}

Code on Rust playground (293 ms)

It calculates dynamic time warping distance between two double vectors using an update rule which is structured like this:

This code takes 293 milliseconds to run on a particular input data. The speedup from 435 milliseconds stated in the previous post is due to Moore’s law: I’ve upgraded the CPU :)

We can bring run time down by tweaking how we calculate the minimum of three elements.

fn min2(x: f64, y: f64) -> f64 {
    if x < y { x } else { y }
}

fn dtw(xs: &[f64], ys: &[f64]) -> f64 {
    // ...
            let d = min2(min2(d11, d10), d01);
    // ...
}

Code on Rust playground (210 ms)

This version takes only 210 milliseconds, presumably because the minimum of two elements in the previous row can be calculated without waiting for the preceding element in the current row to be computed.

The assembly for the main loop looks like this (AT&T syntax, destination register on the right)

   18.32    vmovsd -0x8(%rax,%rsi,8),%xmm1
    0.00    vminsd (%rax,%rsi,8),%xmm1,%xmm1
    6.72    vminsd %xmm0,%xmm1,%xmm0
    4.64    vmovsd -0x8(%r12,%r10,8),%xmm1
    0.00    vsubsd -0x8(%r13,%rsi,8),%xmm1,%xmm1
    7.69    vmulsd %xmm1,%xmm1,%xmm1
   36.14    vaddsd %xmm1,%xmm0,%xmm0
   14.16    vmovsd %xmm0,(%rdi,%rsi,8)

Check the previous post for more details!

The parallel plan

Can we loosen dependencies between cells even more to benefit from instruction level parallelism? What if instead of filling the table row by row, we do it diagonals?

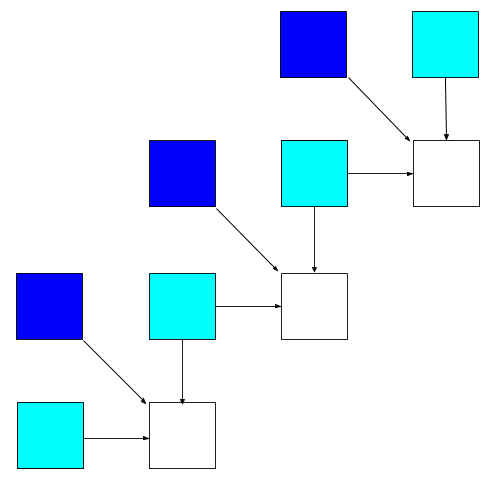
We’d need to remember two previous diagonals instead of one previous row, but all the cells on the next diagonal would be independent! In theory, compiler should be able to use SIMD instructions to make the computation truly parallel.

Implementation Plan

Coding up this diagonal traversal is a bit tricky, because you need to map linear vector indices to diagonal indices.

The original indexing worked like this:

        iy
       ---->
    | . . . .
 ix | . . . .
    | . . . .
    V . . . .

ix and iy are indices in the input vectors.
The outer loop is over ix.
On each iteration, we remember two rows (curr and prev in the code).

For our grand plan, we need to fit a rhombus peg in a square hole:

   id
  ---->
 . . . .        |
   . . . .      | ix
     . . . .    |
       . . . .  V

id is the index of the diagonal. There are twice as much diagonals as rows.
The outer loop is over id.
On each iteration we remember three columns (d1, d2 d3 in the code).
There is a phase transition once we’ve crossed the main diagonal.
We can derive iy from the fact that ix + iy = id.

Code

The actual code looks like this:

fn dtw(xs: &[f64], ys: &[f64]) -> f64 {
    assert_eq!(xs.len(), ys.len());
    let n = xs.len();
    let mut d1 = vec![0f64; n + 1];
    let mut d2 = vec![0f64; n + 1];
    let mut d3 = vec![0f64; n + 1];
    d2[0] = ::std::f64::MAX;

    for id in 1..(2 * n + 1) {
        ::std::mem::swap(&mut d1, &mut d2);
        ::std::mem::swap(&mut d2, &mut d3);

        let ix_range = if id <= n {
            d3[0] = ::std::f64::MAX;
            d3[id] = ::std::f64::MAX;
            1..id
        } else {
            (id - n..n + 1)
        };

        for ix in ix_range {
            let iy = id - ix;
            let d = min2(min2(d2[ix - 1], d2[ix]), d1[ix - 1]);
            let cost = {
                let t = xs[ix - 1] - ys[iy - 1];
                t * t
            };
            d3[ix] = d + cost;
        };
    }

    d3[n]
}

Code on Rust playground (185 ms)

It take 185 milliseconds to run. The assembly for the main loop is quite interesting:

    1.67    cmp    %rax,%rdx
    0.00    jbe    6d95
    1.95    lea    0x1(%rax),%rbx
    8.09    cmp    %rbx,%rdx
    0.98    jbe    6da4
    1.12    cmp    %rax,%r8
    0.00    jbe    6db3
    3.49    cmp    %r12,%rax
    0.00    jae    6de9
    9.07    cmp    %r12,%rcx
    0.00    jae    6dc5
    0.56    cmp    %rbx,%r9
    0.00    jbe    6dd7
    2.23    vmovsd (%r15,%rax,8),%xmm0
   11.72    vminsd 0x8(%r15,%rax,8),%xmm0,%xmm0
    2.09    vminsd (%r11,%rax,8),%xmm0,%xmm0
    2.51    vmovsd (%r14,%rax,8),%xmm1
    7.95    mov    -0x88(%rbp),%rdi
    3.07    vsubsd (%rdi,%rcx,8),%xmm1,%xmm1
    3.91    vmulsd %xmm1,%xmm1,%xmm1
   15.90    vaddsd %xmm1,%xmm0,%xmm0
    8.37    vmovsd %xmm0,0x8(%r13,%rax,8)

First of all, we don’t see any vectorized instructions, the code does roughly the same operations as the in previous version. Also, there is a whole bunch of extra branching instructions on the top. These are bounds checks which were not eliminated this time. And this is great: if I add all off-by one errors I’ve made implementing diagonal indexing, I would get an integer overflow! Nevertheless, we’ve got some speedup.

Can we go further and add get SIMD instructions here? At the moment, Rust does not have a stable way to explicitly emit SIMD (it’s going to change some day) (UPDATE: we have SIMD on stable now!), so the only choice we have is to tweak the source code until LLVM sees an opportunity for vectorization.

SIMD

Although bounds checks themselves don’t slow down the code that much, they can prevent LLVM from vectorizing. So let’s dip our toes into unsafe:

unsafe {
    let d = min2(
        min2(*d2.get_unchecked(ix - 1), *d2.get_unchecked(ix)),
        *d1.get_unchecked(ix - 1),
    );
    let cost = {
        let t =
            xs.get_unchecked(ix - 1) - ys.get_unchecked(iy - 1);
        t * t
    };
    *d3.get_unchecked_mut(ix) = d + cost;
}

Code on Rust playground (52 ms)

The code is as fast as it is ugly: it finishes in whooping 52 milliseconds! And of course we see SIMD in the assembly:

    5.74    vmovupd -0x8(%r8,%rcx,8),%ymm0
    1.44    vminpd (%r8,%rcx,8),%ymm0,%ymm0
    7.66    vminpd -0x8(%r11,%rcx,8),%ymm0,%ymm0
    5.26    vmovupd -0x8(%rbx,%rcx,8),%ymm1
    7.66    vpermpd $0x1b,0x20(%r12),%ymm2
    5.26    vsubpd %ymm2,%ymm1,%ymm1
    7.66    vmulpd %ymm1,%ymm1,%ymm1
    8.61    vaddpd %ymm1,%ymm0,%ymm0
    2.39    vmovupd %ymm0,(%rdx,%rcx,8)
    2.39    vmovupd 0x18(%r8,%rcx,8),%ymm0
    5.74    vminpd 0x20(%r8,%rcx,8),%ymm0,%ymm0
    9.09    vminpd 0x18(%r11,%rcx,8),%ymm0,%ymm0
    0.96    vmovupd 0x18(%rbx,%rcx,8),%ymm1
    4.78    vpermpd $0x1b,(%r12),%ymm2
    3.83    vsubpd %ymm2,%ymm1,%ymm1
    3.83    vmulpd %ymm1,%ymm1,%ymm1
   10.53    vaddpd %ymm1,%ymm0,%ymm0
    4.78    vmovupd %ymm0,0x20(%rdx,%rcx,8)

Safe SIMD

How can we get the same results with safe Rust? One possible way is to use iterators, but in this case the resulting code would be rather ugly, because you’ll need a lot of nested .zip’s. So let’s try a simple trick of hoisting the bounds checks of the loop. The idea is to transform this:

for i in 0..n {
    assert i < xs.len();
    xs.get_unchecked(i);
}

into this:

assert xs.len() < n;
for i in 0..n {
    xs.get_unchecked(i);
}

In Rust, this is possible by explicitly slicing the buffer before the loop:

let ix_range = if id <= n {
    d3[0] = ::std::f64::MAX;
    d3[id] = ::std::f64::MAX;
    1..id
} else {
    (id - n..n + 1)
};

let ix_range_1 = ix_range.start - 1..ix_range.end - 1;
let dn = ix_range.end - ix_range.start;

let d1 = &d1[ix_range_1.clone()];
let d2_0 = &d2[ix_range.clone()];
let d2_1 = &d2[ix_range_1.clone()];
let d3 = &mut d3[ix_range.clone()];
let xs = &xs[ix_range_1.clone()];
let ys = &ys[id - ix_range.end..id - ix_range.start];

// All the buffers we access inside the loop
// will have the same length
assert!(
    d1.len() == dn && d2_0.len() == dn && d2_1.len() == dn
    && d3.len() == dn && xs.len() == dn && ys.len() == dn
);

for i in 0..dn { // so hopefully LLVM can eliminate bounds checks.
    let d = min2(min2(d2_0[i], d2_1[i]), d1[i]);
    let cost = {
        let t = xs[i] - ys[ys.len() - i - 1];
        t * t
    };
    d3[i] = d + cost;
};

Code on Rust playground (107 ms)

This is definitely an improvement over the best safe version, but is still twice as slow as the unsafe variant. Looks like some bounds checks are still there! It is possible to find them by selectively using unsafe to replace some indexing operations.

And it turns out that only ys is still checked!

let t = xs[i] - unsafe { ys.get_unchecked(ys.len() - i - 1) };

Code on Rust playground (52 ms)

If we use unsafe only for ys, we regain all the performance.

LLVM is having trouble iterating ys in reverse, but the fix is easy: just reverse it once at the beginning of the function:

let ys_rev: Vec<f64> = ys.iter().cloned().rev().collect();

Code on Rust playground (50 ms)

Conclusions

We’ve gone from almost 300 milliseconds to only 50 in safe Rust. That is quite impressive! However, the resulting code is rather brittle and even small changes can prevent vectorization from triggering.

It’s also important to understand that to allow for SIMD, we had to change the underlying algorithm. This is not something even a very smart compiler could do!