Min of Three Mar 12, 2017

Test subject

We will be measuring dynamic time warping algorithm. This algorithm calculates a distance between two real number sequences, xs and ys. It is very similar to edit distance or Needleman–Wunsch, because it uses the same dynamic programming structure.

The main equation is

dtw[i, j] =
    min(dtw[i-1, j-1], dtw[i, j-1], dtw[i-1, j]) + (xs[i] - ys[j])^2

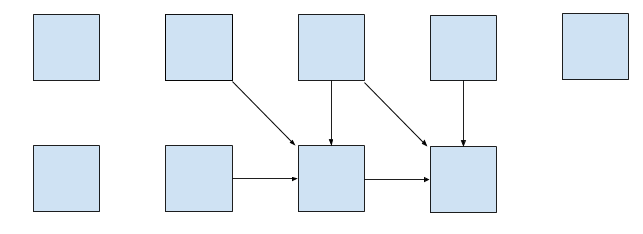
That is, we calculate the distance between each pair of prefixes of xs and ys using the distances from three smaller pairs. This calculation can be represented as a table where each cell depends on three others:

It is possible to avoid storing the whole table explicitly. Each row depends only on the previous one, so we need to store only two rows at a time.

Here is the Rust code for this version:

fn dtw(xs: &[f64], ys: &[f64]) -> f64 {
    // assume equal lengths for simplicity
    assert_eq!(xs.len(), ys.len());
    let n = xs.len();
    let mut prev = vec![0f64; n + 1];
    let mut curr = vec![std::f64::MAX; n + 1];
    curr[0] = 0.0;

    for ix in 1..(n + 1) {
        std::mem::swap(&mut curr, &mut prev);
        curr[0] = std::f64::MAX;
        for iy in 1..(n + 1) {
            let d11 = prev[iy - 1];
            let d01 = curr[iy - 1];
            let d10 = prev[iy];

            // Find the minimum of d11, d01, d10
            // by enumerating all the cases.
            let d = if d11 < d01 {
                if d11 < d10 { d11 } else { d10 }
            } else {
                if d01 < d10 { d01 } else { d10 }
            };

            let cost = {
                let t = xs[ix - 1] - ys[iy - 1];
                t * t
            };

            curr[iy] = d + cost;
        }
    }
    curr[n]
}

Code on Rust playground

Profile first

Is it fast? If we compile it in --release mode with

[build]
rustflags = "-C target-cpu=native"

in ~/.cargo/config, it takes 435 milliseconds for two random sequences of length 10000.

What is the bottleneck? Let’s look at the instruction level profile of the main loop using perf annotate command:

   // Find the minimum of three numbers.
    0.00 :       vmovsd -0x8(%rax,%rsi,8),%xmm1
    0.00 :       vmovsd (%rax,%rsi,8),%xmm2
    0.06 :       vminsd %xmm2,%xmm1,%xmm3
    9.04 :       vminsd %xmm2,%xmm0,%xmm2
    0.00 :       vcmpltsd %xmm0,%xmm1,%xmm0
   22.70 :       vblendvpd %xmm0,%xmm3,%xmm2,%xmm0

   // Calculate the squared error penalty.
    0.00 :       vmovsd -0x8(%r12,%r10,8),%xmm1
    0.00 :       vsubsd -0x8(%r13,%rsi,8),%xmm1,%xmm1
   11.01 :       vmulsd %xmm1,%xmm1,%xmm1

   // Store the result in the `curr` array.
   // Note how xmm0 is used on the next iteration.
   22.81 :       vaddsd %xmm1,%xmm0,%xmm0
   10.67 :       vmovsd %xmm0,(%rdi,%rsi,8)

perf annotate uses AT&T assembly syntax, this means that the destination register is on the right.

The xmm0 register holds the value of curr[iy], which was calculated on the previous iteration. Values of prev[iy - 1] and prev[iy] are fetched into xmm1 and xmm2. Note that although the original code contained three if expressions, the assembly does not have any jumps and instead uses two min and one blend instruction to select the minimum. Nevertheless, a significant amount of time, according to perf, is spent calculating the minimum.

Optimization

Can we do better? Let’s use min2 function to calculate minimum of three elements recursively:

fn min2(x: f64, y: f64) -> f64 {
    if x < y { x } else { y }
}

fn dtw(xs: &[f64], ys: &[f64]) -> f64 {
    // ...
            let d = min2(min2(d11, d01), d10);
    // ...
}

Code on Rust playground

This version completes in 430 milliseconds, which is a nice win of 5 milliseconds over the first version, but is not that impressive. The assembly looks cleaner though:

    0.00 :       vmovsd -0x8(%rax,%rsi,8),%xmm1
    0.28 :       vminsd %xmm0,%xmm1,%xmm0
   31.14 :       vminsd (%rax,%rsi,8),%xmm0,%xmm0

    0.06 :       vmovsd -0x8(%r12,%r10,8),%xmm1
    0.28 :       vsubsd -0x8(%r13,%rsi,8),%xmm1,%xmm1
   10.61 :       vmulsd %xmm1,%xmm1,%xmm1

   23.29 :       vaddsd %xmm1,%xmm0,%xmm0
   11.11 :       vmovsd %xmm0,(%rdi,%rsi,8)

Up to this point it was a rather boring blog post about Rust with some assembly thrown in. But let’s tweak the last variant just a little bit …

fn dtw(xs: &[f64], ys: &[f64]) -> f64 {
    // ...
            // Swap d10 and d01.
            let d = min2(min2(d11, d10), d01);
    // ...
}

Code on Rust playground

This version takes only 287 milliseconds to run, which is roughly 1.5 times faster than the previous one! However, the assembly looks almost the same …

    0.08 :       vmovsd -0x8(%rax,%rsi,8),%xmm1
    0.17 :       vminsd (%rax,%rsi,8),%xmm1,%xmm1
   16.40 :       vminsd %xmm0,%xmm1,%xmm0

    0.00 :       vmovsd -0x8(%r12,%r10,8),%xmm1
    0.17 :       vsubsd -0x8(%r13,%rsi,8),%xmm1,%xmm1
   18.24 :       vmulsd %xmm1,%xmm1,%xmm1

   17.15 :       vaddsd %xmm1,%xmm0,%xmm0
   15.82 :       vmovsd %xmm0,(%rdi,%rsi,8)

The only difference is that two vminsd instructions are swapped. But it is definitely much faster.

A possible explanation

A possible explanation is a synergy of CPU level parallelism and speculative execution. It was proposed by @krdln and @vitalyd. I don’t know how to falsify it, but it at least looks plausible to me!

Imagine for a second that instead of vminsd %xmm0,%xmm1,%xmm0 instruction in the preceding assembly there is just vmovsd %xmm1,%xmm0. That is, we don’t use xmm0 from the previous iteration at all! This corresponds to the following update rule:

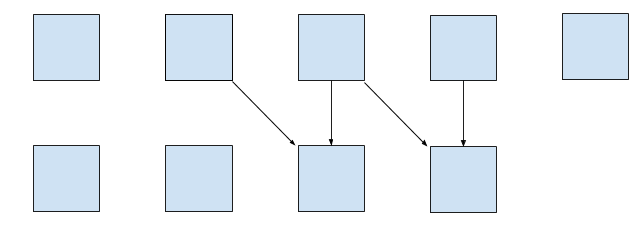
The important property of this update rule is that CPU can calculate two cells simultaneously in parallel, because there is no data dependency between curr[i] and curr[i + 1].

We do have vminsd %xmm0,%xmm1,%xmm0, but it is equivalent to vmovsd %xmm1,%xmm0 if xmm1 is smaller than xmm0. And this is often the case: xmm1 holds the minimum of upper and diagonal cell, so it is likely to be less then a single cell to the left. Also, the diagonal path is taken slightly more often then the two alternatives, which adds to the bias.

So it looks like the CPU is able to speculatively execute vminsd and parallelise the following computation based on this speculation! Isn’t that awesome?

Further directions

It’s interesting that we can make the computation truly parallel if we update the cells diagonally:

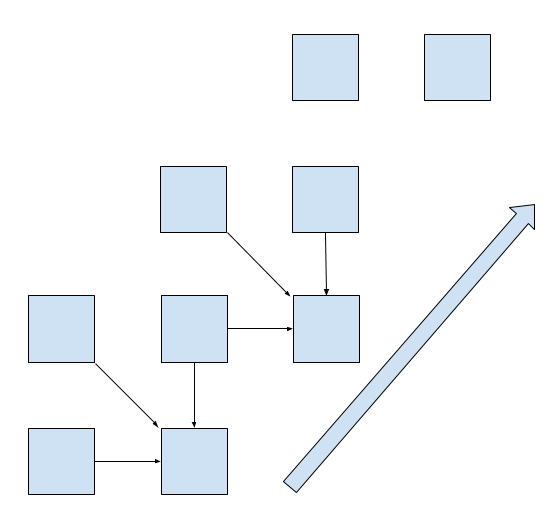
This is explored in the second part of this post.

Conclusion

Despite the fact that Rust is a high level language, there is a strong correlation between the source code and the generated assembly. Small tweaks to the source result in the small changes to the assembly with potentially big implications for performance. Also, perf is great!

That’s all :)